정보의 표현 단위와 수 체계(2,8,10,16진법)
비트(bit) : 2진수로 데이터를 표현하는 단위, n비트로 2진수 2의 n승 개를 표현할 수 있다.

바이트(byte) : 정보를 표현하기 위한 비트의 집합으로 1바이트 = 8비트 이다.
문자를 2진수로 표현하는 대표적인 표준 코드인 ASCII(American Standard Code for Information Interchange)코드의
경우 한 문자가 8비트로 이루어져 1바이트가 한 문자라는 개념으로 정보가 처리된다.
워드(word) : 컴퓨터의 종류에 따라 2, 4, n바이트 등으로 구성되며 일반적으로 32비트(4바이트)가 많이 쓰인다.

2진수의 비트는 위 표 2-2와 같이 나타낼 수 있다.
킬로, 메가, 기가, 테라... 컴퓨터를 접하면서 저장장치의 용량으로 꽤나 많이 들어왔던 단위들이다.
- 수 체계
수를 나타내기 위해 약속한 기호와 규칙을 통틀어 수 체계(number system)라고 한다.
수 체계는 실제로 존재하는 수인 실수(real number)와 상상의 수 또는 가공의 수인 허수(imainary number)가
존재하며 이 둘을 합쳐서 복소수(complex number)라고 한다.
실수 중 유리수(rational number)는 두 정수의 비로 나타낼 수 있는 수이고,
무리수(irrational number)는 두 정수의 비로 나타낼 수 없는 수이다.
유리수는 다시 정수(integer)와 정수가 아닌 유리수로 구분된다.
그리고 정수는 다시 양수(positive number)와 음수(negative number), 0으로 구분되는데 양수는 양의 값인 정수, 음수는
음의 값인 정수이다. 또한 정수가 아닌 유리수 중 분수는 나누어진 수를 의미하며, 소수(decimal fraction)는 1보다 작고
0보다 큰 수를 말한다.

수 체계는 자릿수 체계와 비자릿수 체계로 구분하며 자릿수 체계에는 2, 8, 10, 16진법 등이 있으며, 컴퓨터와 같은
디지털 장치는 기호 2개로 수를 표현하므로 2진법을 사용한다.
- 10진법
0부터 9까지 10개의 수로 표현하는 10진법(decimal notation)은 각 자리에서 9 다음에 자리 올림이 발생하고, 각 자리의
단위가 10의 지수승(10의 N승)이다. 10진법으로 나타낸 수를 10진수라고 하며, 다른 진법으로 나타낸 진수와 구별하기
위해 첨자 10으로 표시한다.
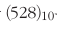

- 2진법
0과 1로 수를 표현하는 2진법(binary notation)은 각 자리의 단위가 2의 지수승(2의 N승)이다.
2진법으로 나타낸 수를 2진수라고 하며, 다른 진법으로 나타낸 진수와 구별하기 위해 첨자 2로 표시한다.

- 8진법
8을 기수로 한 숫자의 체계로 숫자는 0~7이 사용되고 2진수(binary number)를 단축하는 경우에 자주 사용된다. 이 8진법 기수가 2의 제곱승이라는 것으로 컴퓨터의 경우 10진수보다 편리하다.
- 16진법
16을 고정된 기초로 하는 수의 표기법으로 16진법은 기계 제어용 컴퓨터 등에 사용되고 있다.

- 2진수 ▶ 10진수 변환

2진수를 10진수로 변환하는 방법이다.
가장 오른쪽 부터 왼쪽으로 2^0, 2^1, 2^2 ... 순으로 승수가 커진다.
그리고 자리마다 1이면 2^n x 1, 0이면 2^n x 0으로 각 자리마다 계산을 한 후
서로 더해주면 된다.
- 2진수 ▶ 8진수 변환

2진수를 8진수로 변환하는 방법이다.
일단 맨 오른쪽부터 세 자리씩 끊는다.
그리고 맨 왼쪽 1이 딱 하나가 남는데 이럴 경우는 앞에 0을 2개 붙여준다.
그리고 2진수를 10진수로 변환했던 것 처럼 계산을 해준 후
숫자들을 서로 붙여주면 된다. (덧셈 X)
- 2진수 ▶ 16진수 변환

2진수를 16진수로 변환하는 방법이다.
기본적인 방법은 2진수를 8진수로 변환할 때 썼던 방법과 똑같다.
다만 16진수는 맨 오른쪽부터 네 자리씩 끊어준다.
이후 방법은 동일.
16진수에서는 10진수 기준 '10'부터 '15'까지 알파벳으로 표기를 한다.
Ex) 10 = A, 11 = B, 12 = C, 13 = D, 14 = E, 15 = F
진수표를 참고하여 작성하도록 하자.
- n진수 ▶ 2진수 변환

이번엔 반대로 8, 10, 16진수에서 2진수로의 변환 방법이다.
여긴 간단하다. 그냥 각 진법으로 표기된 수를 '2'로 더 이상 나눠지지
않을 때 까지 나눠주고 맨 마지막 몫을 제일 앞자리에 적어주고 나머지를
역순으로 올려 적어주면 2진수로의 변환을 할 수 있다.